Los conceptos básicos de población y muestra.
Colección de datos.
Población y muestra.
Estadística descriptiva y de inferencia.
1. INTRODUCCIÓN
Existen diferentes razones por las cuales los profesionales de la educación deben tener un buen conocimiento sobre probabilidad y estadística y tenerla como instrumentos del trabajo cotidiano.
Entre dichas razones señalamos las siguientes:
• Trabajar concepciones con análisis de los materiales y recursos para el aula.
• También para realizar trabajos teóricos, metodológicos y relacionados.
• Despierta capacidad crítica objetiva para detectar errores potenciales.
• Nos será también útil para llegar a conclusiones correctas acerca de procedimientos y alcanzar resultado optimo.
Resulta imprescindible, por lo tanto, conocer los conceptos básicos de estadística que nos faciliten la realización de estudios y conocer las posibilidades a desarrollar con ayuda de profesionales estadísticos para mejorar dicho análisis.
Este curso pretende dar a conocer algunas nociones estadísticas que nos ayudarán a explorar y describir, nuestros datos.
2. ESTADÍSTICA
Se define la Estadística como:
"Ciencia que se ocupa del estudio de fenómenos de tipo genérico, normalmente complejos y enmarcados en un universo variable, mediante el empleo de modelos de reducción de la información y de análisis de validación de los resultados en términos de representatividad.“
3. POBLACIÓN Y MUESTRA
Cuando se realiza un estudio de investigación, se pretende generalmente inferir o generalizar resultados de una muestra a una población. Se estudia en particular a un reducido número de individuos a los que tenemos acceso con la idea de poder generalizar los hallazgos a la población de la cual esa muestra procede.
Este proceso de inferencia se efectúa por medio de métodos estadísticos basados en la probabilidad.

•La población
Representa el conjunto grande de individuos que deseamos estudiar y generalmente suele ser inaccesible.
Es, en definitiva, un colectivo homogéneo que reúne unas características determinadas.
• La muestra
Es el conjunto menor de individuos (subconjunto de la población accesible y limitado sobre el que realizamos las mediciones o el experimento con la idea de obtener conclusiones generalizables a la población ).
El individuo es cada uno de los componentes de la población y la muestra. La muestra debe ser representativa de la población y con ello queremos decir que cualquier individuo de la población en estudio debe haber tenido la misma probabilidad de ser elegido.

•Las razones para estudiar muestras en lugar de poblaciones son diversas y entre ellas podemos señalar:
a) Ahorrar tiempo y costo. Se invierte en menos individuos.
b) Es más posible de abarcar. Estudiar la totalidad a las personas con una característica determinada en muchas ocasiones puede ser una tarea inaccesible o imposible de realizar.
c) Aumentar la calidad del estudio. Al disponer de más tiempo y recursos, las observaciones y mediciones realizadas a un reducido número de individuos pueden ser más exactas y plurales que si las tuviésemos que realizar a una población
d) Permite reducir la heterogeneidad de una población. La selección de muestras específicas nos al indicar los criterios de inclusión y/o exclusión.
 4. Estadística Descriptiva
4. Estadística Descriptiva
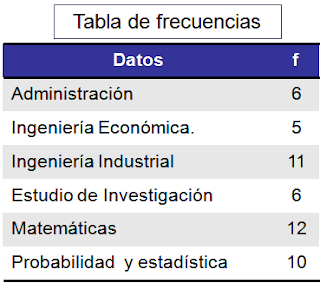
Una vez que se han recogido los valores que toman las variables de nuestro estudio (datos), procederemos al análisis descriptivo de los mismos. Para variables categóricas, como el sexo, se quiere conocer el número de casos en cada una de las categorías, reflejando Habitualmente el porcentaje que representan del total, y expresándolo en una tabla de frecuencias.
•Los datos pueden ser resumidos numérica o gráficamente. Ejemplos básicos de descriptores numéricos son: la media y la desviación estándar. Resúmenes gráficos incluyen varios tipos de figuras y gráficos.
La descriptiva presenta la información en forma cómoda, utilizable y comprensible
5. LOS DATOS
Lo que estudiamos en cada individuo de la muestra son las variables (edad, sexo, peso, talla,).
Los datos son los valores que toma la variable en cada caso.
Lo que vamos a realizar es medir, es decir, asignar valores a las variables incluidas en el estudio.
Deberemos además concretar la escala de medida que aplicaremos a cada variable.
La naturaleza de las observaciones será de gran importancia a la hora de elegir el método estadístico más apropiado para abordar su análisis. con este fin, Clasificaremos las variables, a grandes rasgos, en dos tipos;
Variables cuantitativas o Variables cualitativas.
•Variables cualitativas. una cualidad o atributo que clasifica a cada caso en una de varias categorías.
• Variables Cuantitativas. Son las variables que pueden medirse, cuantificarse o expresarse numéricamente.
Las variables cuantitativas pueden ser de dos tipos:
a. Variables Cuantitativas Continuas, si admiten tomar cualquier valor dentro de un rango numérico determinado (edad, peso, talla).
Ejemplo de Variables Continua
Tiempo para resolver un examen.
Máxima temperatura ambiental durante el día
Litros de gasolina vendidos el anterior en una gasolinera.
Altura del mercurio en un barómetro
b. Variables Cuantitativas Discretas, si no admiten todos los valores intermedios en un rango. Suelen tomar solamente valores enteros (número de hijos, número de aprobados por materia, número de hermanos, etc).
Ejemplo de Variables Discreta
Número de águilas en 6 lanzamientos de una moneda
Número de dientes de un niño
Número de juegos ganados por un equipo de basketball
Número de hijos de una familia.
El proceso de medición de las variables
•En el proceso de medición de las variables, se pueden utilizar dos escalas:
a.Escalas Nominales: ésta es una forma de observar o medir en la que los datos se ajustan por categorías que no mantienen una relación de orden entre sí (color de los ojos, sexo, profesión, etcétera).
b.Escalas Ordinales: en las escalas utilizadas, existe un cierto orden o jerarquía entre las categorías (notas en los exámenes).