Recta de Regresión.

Coeficiente de correlación


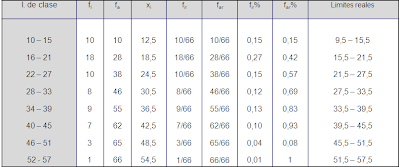
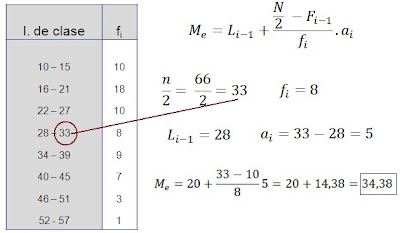
El coeficiente de correlación lineal es el cociente entre la covarianza y el producto de las desviaciones típicas de ambas variables.


El coeficiente de correlación lineal se expresa mediante la letra r.

Si la correlación es nula, r = 0, las rectas de regresión son perpendiculares entre sí, y sus ecuaciones son:

Recta de regresiónLa recta de regresión es la que mejor se ajusta a la nube de puntos.

La recta de regresión pasa por el punto promedio llamado centro de gravedad.

Recta de regresión de Y sobre X

La recta de regresión de Y sobre X se utiliza para estimar los valores de la Y a partir de los de la X.

La pendiente de la recta es el cociente entre la covarianza y la varianza de la variable X.

Recta de regresión de X sobre Y

La recta de regresión de X sobre Y se utiliza para estimar los valores de la X a partir de los de la Y.
La pendiente de la recta es el cociente entre la covarianza y la varianza de la variable Y.

Tipificación

• Puntuaciones Típicas
• Puntuaciones diferenciales
• Observaciones sobre puntuaciones típicas
• Ejercicio de puntuaciones típicas

Puntuaciones Típicas

Las puntuaciones diferenciales resultan de restarles a las puntuaciones directas la media aritmética.

Las puntuaciones típicas son el resultado de dividir las puntuaciones diferenciales entre la desviación típica. Este proceso se llama tipificación.

Las puntuaciones típicas se representan por z.

Observaciones sobre puntuaciones típicas

1. Las puntuaciones típicas son el resultado de dividir las puntuaciones diferenciales entre la desviación típica. Este proceso se llama tipificación.
2. La media aritmética de las puntuaciones típicas es 0.
3. La desviación típica de las puntuaciones típicas es 1.
4. Las puntuaciones típicas son adimensionales, es decir, son independientes de las unidades utilizadas.
5. Las puntuaciones típicas se utilizan para comparar las puntuaciones obtenidas en distintas distribuciones.
   Ejercicio de puntuaciones típicas
Una persona A mide 1.75 m y recibe en una ciudad donde la estatura media es de 1.60 m y la desviación típica es de 20 cm. Otra persona B mide 1.80 m y vive en una ciudad donde la estatura media es de 1.70 m y la desviación típica es de 15 cm. ¿Cuál de las dos será más alta respecto a sus conciudadanos?

La persona A es más alta respecto a sus conciudadanos que la persona B.

http://www.aulademate.com/contentid-289.html

Cálculo de medidas de posición

Ejercicio para  datos agrupados

Calcular los cuartiles, deciles, percentil 35 y el percentil 60 de la distribución de la tabla:

Cálculo de los cuartiles

Cálculo de los deciles

Calcular los percentil 35 y 60

Medidas de Posición

Las Medidas de Posición

Los Cuartiles

Los cuartiles son los tres valores de la variable que dividen a un conjunto de datos ordenados en cuatro partes iguales.

Son valores de la variable que dividen a la distribución en 4 partes, cada una de las cuales engloba el 25 % de las mismas.

Cálculo de los cuartiles para  datos NO agrupados

1 Ordenamos los datos de menor a mayor.

2 Buscamos el lugar que ocupa cada cuartil mediante la expresión 

Cálculo de los cuartiles para  datos agrupados

En primer lugar buscamos la clase donde se encuentra en la tabla de las frecuencias acumuladas. 

Deciles ( Di)

Son los valores de la variable que dividen a la distribución en las partes iguales, cada una de las cuales engloba el 10 % de los datos.

En total habrá 9 deciles.

(Q2 = D5 = Me ) 

Cálculo de los Deciles para datos agrupados

En primer lugar buscamos la clase donde se encuentra, en la tabla de las frecuencias acumuladas

Centiles o Percentiles ( Pi) 

Los percentiles son los 99 valores que dividen la serie de datos en 100 partes iguales.

Los percentiles dan los valores correspondientes al 1%, al 2%... y al 99% de los datos.

P50 coincide con la mediana.

Cálculo de los Percentiles para datos agrupados

Análisis Estadístico con las MEDIDAS DE DISPERSIÓN

Análisis Estadístico de las Edades de las Personas que Asisten a Cines Unidos Ubicado en el Centro Comercial Regina (CCR) – Puerto La Cruz

Distribución de Frecuencias

Medidas de Dispersión

Gráfico de Dispersión

Desviación media (DM)

Desviación típica (S)

Varianza (S2)

Coeficiente de variación (CV)

Coeficiente de Shepeard (CS)

Medidas de dispersión

Una medida del grado de variación de un conjunto de valores de una variable estadística la proporciona el propio rango o recorrido de la variable.

 Lo mas frecuente, sin embargo, es describir esa variación mediante las diferencias entre esos valores y alguna medida de tendencia central.

Para las variables cuantitativas, las medidas de dispersión mas utilizadas son la desviación media y la desviación típica. 

Desviación media (DM)

Se conoce también como promedio de desviación. Es igual a la media aritmética de las desviaciones de una serie de valores respecto de su media aritmética. Para una serie de N valores: X1, X2, X3,… Xn, se define a través de la siguiente expresión: 

Desviación típica (S):

Se define como la raíz cuadrada positiva del promedio aritmético de los cuadrados de los desvíos con respecto a la medida aritmética y se considera como el indicador de variación o dispersión más importante. 

Coeficiente de variación (CV)

Se define como el cociente que resulta de dividir la desviación típica entre la medida aritmética de la serie de datos, multiplicado luego por cien para que su resultado venga expresado en porcentaje.

Varianza (S2)

La varianza se define como el cuadrado de la desviación típica. Su mayor utilidad se presenta en la estadística inductiva. Se puede determinar como una medida de variación promedio y se obtiene dividiendo la variación total por el número de medidas.

Coeficiente de Shepeard (CS)

Se define como el cociente que resulta de dividir el intervalo de clases al cuadrado entre doce para luego restarlo con la varianza para ser utilizado en las distribuciones cuando ya se debe haber hecho un examen completo de la situación.

 

Análisis de datos

Análisis Estadístico de una serie de datos, hallar:

• Polígono e Histograma de Frecuencia Simple.

•Diagrama circular de frecuencias simple.

•Polígono e Histograma de Frecuencia Acumulada 

•Diagrama circular de frecuencias acumuladas.

•Medidas de Tendencia Central.

Análisis Estadístico de las Edades de las Personas que Asisten a Cines Unidos Ubicado en el Centro Comercial Regina (CCR) – Puerto La Cruz

Tabla de Distribución de Frecuencias

Polígono e Histograma de Frecuencia Simple

Diagrama circular de frecuencias simple.

Polígono e Histograma de Frecuencia Acumulada

Diagrama circular de frecuencias acumuladas.

Medidas de Tendencia Central.

Media aritmética

Para datos agrupados

Medidas de Tendencia Central.

Moda

Para datos agrupados

Medidas de Tendencia Central.

Mediana

Para datos agrupados